En tant que mécanisme de transmission, l'engrenage planétaire est largement utilisé dans diverses applications d'ingénierie, telles que les réducteurs de vitesse, les grues, etc. Dans les réducteurs planétaires, il peut remplacer le système de transmission à essieu fixe dans de nombreux cas. Le processus de transmission par engrenages étant un contact linéaire, un engrènement prolongé peut entraîner une défaillance ; il est donc nécessaire de simuler leur résistance. Li Hongli et al. ont utilisé une méthode de maillage automatique pour mailler l'engrenage planétaire et ont obtenu une relation linéaire entre le couple et la contrainte maximale. Wang Yanjun et al. ont également maillé l'engrenage planétaire par une méthode de génération automatique et ont réalisé des simulations statiques et modales. Dans cet article, des éléments tétraédriques et hexaédriques sont principalement utilisés pour le maillage, et les résultats finaux sont analysés afin de vérifier si les conditions de résistance sont respectées.

1. Établissement du modèle et analyse des résultats

Modélisation tridimensionnelle d'un engrenage planétaire

Engrenage planétaireCe train épicycloïdal est principalement composé d'une couronne dentée, d'un pignon solaire et d'un train planétaire. Les principaux paramètres retenus dans cette étude sont les suivants : la couronne dentée comporte 66 dents, le pignon solaire 36 dents et le train planétaire 15 dents. Le diamètre extérieur de la couronne dentée est de 150 mm, le module d'Young de 2 mm, l'angle de pression de 20°, la largeur de dent de 20 mm, le coefficient de hauteur d'addendum de 1 et le coefficient de jeu de 0,25. Le train épicycloïdal comprend trois engrenages.

Analyse par simulation statique d'un engrenage planétaire

Définir les propriétés des matériaux : importer le système d’engrenages planétaires tridimensionnel dessiné dans le logiciel UG dans ANSYS et définir les paramètres des matériaux, comme indiqué dans le tableau 1 ci-dessous :

Maillage : Le maillage par éléments finis est composé de tétraèdres et d’hexaèdres, et la taille de base des éléments est de 5 mm.engrenage planétaireLa roue solaire et la couronne dentée intérieure sont en contact et en prise. Le maillage des zones de contact et d'engrènement est densifié, avec un pas de 2 mm. Dans un premier temps, un maillage tétraédrique est utilisé (figure 1), générant 105 906 éléments et 177 893 nœuds. Ensuite, un maillage hexaédrique est adopté (figure 2), générant 26 957 cellules et 140 560 nœuds.

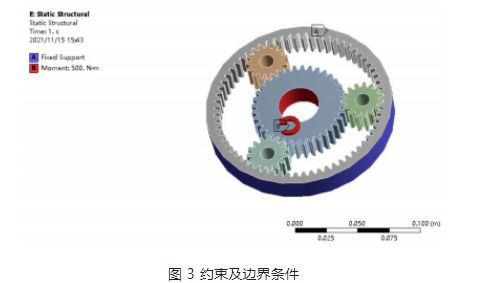
Application de la charge et conditions aux limites : compte tenu des caractéristiques de fonctionnement du train épicycloïdal du réducteur, la roue solaire est l’engrenage menant, le train épicycloïdal est l’engrenage mené et la sortie finale est assurée par le porte-satellites. Fixez la couronne intérieure dans ANSYS et appliquez un couple de 500 N·m à la roue solaire, comme illustré sur la figure 3.

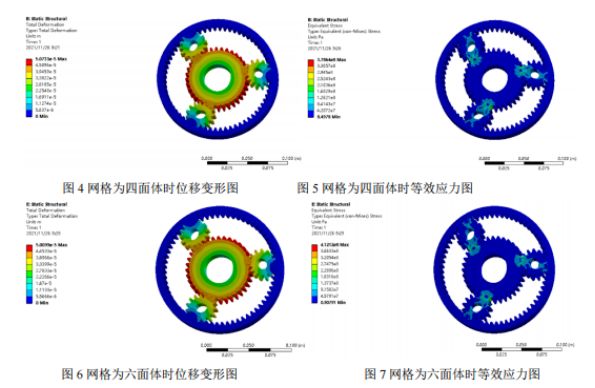
Post-traitement et analyse des résultats : Les néphogrammes de déplacement et de contrainte équivalente de l’analyse statique, obtenus à partir de deux maillages, sont présentés ci-dessous et une analyse comparative est effectuée. L’analyse des néphogrammes de déplacement des deux types de maillages révèle que le déplacement maximal se produit à l’endroit où la roue solaire ne s’engrène pas avec la roue planétaire, et que la contrainte maximale se situe à la base de l’engrènement. La contrainte maximale du maillage tétraédrique est de 378 MPa, et celle du maillage hexaédrique de 412 MPa. La limite d’élasticité du matériau étant de 785 MPa et le coefficient de sécurité de 1,5, la contrainte admissible est de 523 MPa. Les contraintes maximales obtenues sont inférieures à la contrainte admissible, et les conditions de résistance sont donc respectées.

2. Conclusion

Grâce à la simulation par éléments finis de l'engrenage planétaire, on obtient le néphogramme de déformation par déplacement et le néphogramme de contrainte équivalente du système d'engrenage, à partir desquels on détermine les valeurs maximales et minimales ainsi que leur distribution.engrenage planétaireUn modèle peut être trouvé. L'emplacement de la contrainte équivalente maximale correspond également à l'endroit où les dents d'engrenage sont les plus susceptibles de se rompre ; il convient donc d'y accorder une attention particulière lors de la conception ou de la fabrication. L'analyse de l'ensemble du système d'engrenage planétaire permet de corriger l'erreur due à l'analyse d'une seule dent.